Trouver un chemin, ou même le plus court chemin, est un problème courant en informatique. Parmi les applications concrètes de ce problème, on peut tout d’abord penser à l’itinéraire le plus court, donné par un dispositif GPS. Ce n’est cependant pas la seule application réelle. On peut par exemple chercher un plus court chemin pour une IA dans un jeu ou encore trouver la manière la plus rapide de mettre deux personnes en relation dans un réseau professionnel.

Un problème facile ?

Le problème du plus court chemin est un problème très connu et très étudié. En réalité, il y a pleins de variantes possibles. Certaines peuvent être faciles à résoudre, comme trouver le meilleur itinéraire avec un GPS. D’autres au contraire peuvent être extrêmement difficiles, comme trouver le chemin le plus court passant par un ensemble de villes, pour effectuer des livraisons par exemple (problème du voyageur de commerce/tournées de véhicules). Nous allons voir ici un algorithme simple pour résoudre un problème similaire à celui de l’itinéraire.

Présentation du problème

Imaginons que nous connaissons certaines personnes qui détiennent une même information cruciale que nous voulons récupérer. Le soucis est que ces personnes ne nous donneront pas ce message directement, par manque de confiance. En effet, elle ne font confiance qu’à leurs amis directs et le confieront seulement à eux.

Si on considère notre cercle d’amis, nous sommes connectés à un certain nombre de personnes qui sont elles-même connectées à d’autres personnes par des relations d’amitié. Notre défi est de récupérer cette information le plus rapidement possible, en la faisant transmettre d’amis en amis. Pour ce faire, nous allons donc demander à nos amis proches de demander a leurs amis de demander à leurs amis etc… jusqu’à ce qu’un personne diffuse l’information dans le sens inverse pour qu’elle revienne vers nous.

L’objectif est donc de trouver le lien le plus court entre nous et l’information, c’est à dire de trouver une suite de personne Alice - Bob - Charles - … la plus courte telle que deux personnes successives sont amies, la première personne de la liste étant nous et la dernière étant une personne qui détient l’info.

Détour par les graphes

Les données de notre problèmes constituent un réseau d’amis. Nous avons les noms des personnes, ainsi que leurs relations, c’est à dire avec quelles autres personnes elle sont amies. Une bonne façon de manipuler nos données est de les représenter sous forme d’un graphe.

Un graphe est un objet mathématique qui peut être utilisé pour manipuler des données comportant une relation. Cet objet est constitué de sommets (ici les différentes personnes) et d’arêtes, qui représentent les liens entre les différents sommets (ici ce sont les liens d’amitié).

Algorithme de résolution

L’algorithme de résolution du problème est un algorithme qui effectue un parcours en largeur du graphe. Cela signifie qu’il va parcourir tous les sommets du graphe, en commençant du plus proches du sommet de départ au plus éloignés. Dire que deux sommets sont proches signifie ici qu’ils sont connectés par un petit nombre d’arêtes.

Déroulement de l’algorithme

L’algorithme utilise une file d’attente (souvent appelé file en info) contenant les sommets (amis) à visiter. Au tout début, cette file d’attente contient le sommet qui nous réprésente dans le graphe. Ensuite, une même étape est répétée tant que la file d’attente n’est pas vide : le premier sommet ajouté dans la file est retiré et l’algorithme vérifie si il contient l’info recherchée. Si c’est le cas, il peut s’arrêter, sinon il retire ce sommet et ajoute tous les amis de ce sommet. Une seule règle doit être respectée : les amis d’un sommet sont ajoutés à la file uniquement s’ils n’ont pas déjà été visités par l’algorithme.

L’algorithme va donc parcourir progressivement le graphe en partant d’un sommet et en allant vers ses amis. Concrètement, il va d’abord considérer le premier sommet, celui qui nous correspond. Il va ensuite chercher tous les amis de ce sommet et les ajouter à une file d’attente. Ces amis seront ensuite considérés et l’algorithme va vérifier si l’info est détenu par l’un d’eux. Enfin les amis de cet ami considéré seront ajoutés à la file d’attente également.

Il y a encore une chose dont on a pas parlé. Avec les étapes précédentes, on est capable de trouver l’info mais on ne peut pas encore afficher le chemin qui permet de l’atteindre (c’est à dire la liste des personnes). On a cependant déjà fait le plus gros du travail. Pour retrouver le chemin on procède en plusieurs étapes. Dans une premier temps, on indique pour chaque sommet à partir de quel sommet on l’a visité. Par exemple, si on visite le sommet A et on ajoute son ami B à la file, on indique alors que B est obtenu à partir de A. La deuxième étape consiste à prendre le sommet contenant l’info une fois sorti de la boucle, et a remonter successivement vers le sommet d’origine pour finir vers le sommet nous représentant.

Un mot sur les files

L’algorithme que je propose pour résoudre ce problème utilise une structure de donnée appelée file (la fameuse file d’attente). En quelque mots, une file est une liste d’éléments, ici de sommets ou de personnes. Le premier élément est appelé la tête et le dernier la queue.

Elle respecte deux propriétés :

• lorsqu’un élément est ajouté à la file, il est ajouté à la fin et il devient ainsi la queue
• le seul élément qui peut être consulté et retiré est le premier élément, c’est à dire la tête.

Cette structure de donnée est généralement appelée FIFO (First In First Out). En effet, dans une telle structure, c’est le premier élément ajouté dans la file qui sera retiré en premier. Pensez donc à la file d’attente de la caisse d’un magasin. On ne peut s’insérer qu’à la fin de la file (en général!) et c’est la première personne arrivée qui est servie en premier.

Créer les mécanismes d’une file est assez simple. Il y a plusieurs façon de le faire et tous les langages de programmation proposent directement ce genre d’outil.

Algorithme en pseudo code

ajout à file du sommet nous correspondant

TANT QUE l'info n'est pas trouvée et que la file n'est pas vide FAIRE

    sommet <- tête de la file
    retirer la tête de la file

    SI le sommet contient l'info ALORS
        sortir de la boucle
    SINON
        ajouter à la file ses amis non visités
        indiquer aux sommets amis que leur sommet d'origine est le sommet visité
    FIN SI

FIN TANT QUE

SI l'info a été trouvée ALORS
    afficher l'info
    reconstruire le chemin à partir des sommets d'origines
FIN SI  

Explications sur l’algorithme

Il n’est pas forcément évident au premiers abords de comprendre réellement ce que l’algorithme fait. Je rappelle qu’on cherche ici un plus court chemin. Si le chemin trouvé est bien le plus court (ou un des plus court) c’est pour une unique raison. Ce qu’il faut garder à l’esprit, c’est que tous les amis des sommets visités sont ajoutés à la fin de la liste d’attente. Cela signifie qu’ils seront visités seulement après tous les sommets présents avant dans la liste. De plus, les sommets ajoutés en fin de liste auront toujours une distance supérieure à ceux ajoutés avant (la distance est le nombre d’amis intermédiaires qui sépare Moi du sommet). De ce fait, lorsqu’un sommet contenant l’info est trouvé, tous les sommets de distance inférieur ont déjà été visités.

Exemple pas à pas

Voici un exemple de graphe d’amis. Le sommet nous représentant est le sommet Moi et le sommet contenant l’info est le sommet avec la pastille jaune (Jackorah). Nous allons ici dérouler toutes les étapes de la résolution du problème. La liste des sommets d’origines est présente à la fin de l’exemple.

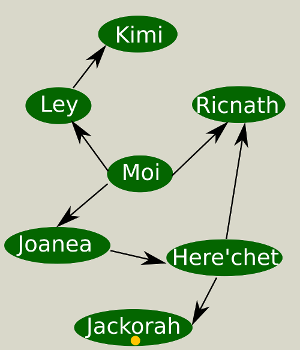
Comme dit précédemment, un tout début, la file d’attente contient uniquement le sommet nous représentant :

-> Moi

On entre ensuite dans la boucle et on retire ce sommet de la file. Ce sommet n’est pas un sommet contenant l’info, on ne sort donc pas de la boucle. On ajoute donc les sommets amis de ce sommet. On n’oublie pas de préciser pour les amis que Moi est leur sommet d’origine. Cela donne :

-> Ley ; Ricnath ; Joanea

Nouveau tour de boucle, l’algorithme retire le premier sommet de la file (le seul accessible pour cette structure de donnée). Manque de chance, Ley ne détient pas l’info non plus, on ajoute donc ses amis à la fin de la file.

-> Ricnath ; Joenea ; Kimi

On recommence encore une fois, cette fois c’est Ricnath qui est visité, il ne détient pas l’info, ses amis sont ajoutés.

-> Joanea ; Kimi ; Here’chet

Au tour de Jonea désormais. Toujours pas d’info, on ajoute ses amis… Ah mince ! Here’chet a déjà été ou est présent dans la file, on ne l’ajoute donc pas !

-> Kimi ; Here’chet

Au tour de Kimi, pas d’info ni d’amis, on passe vite dessus.

-> Here’chet

Le fameux Here’chet désormais. Ah toujours rien ! Mais il a un amis, on l’ajoute donc à la file.

-> Jackorah

Notre dernière chance, car il n’a pas d’amis et si la liste est vide alors l’algo s’arrête. Ouf ! Il a bien l’info, on peut la récupérer.

Voici le tableau des sommets d’origine :

Ceci nous permet donc de reconstruire la liste. On part donc du sommet sur lequel on a trouvé l’info : Jackorah. On remonte vers le sommet d’origine, cela donne Here’chet. On continue avec le sommet d’origine de Here’chet, cela donne Ricnath. Et on termine enfin car le sommet d’origine de Ricnath est Moi.

Finalement on obtient donc la liste : Moi -> Ricnath -> Here’chet -> Jackorah

On a donc une liste de 4 personnes, et il n’est pas possible de faire plus court. On peut néanmoins remarquer qu’il y avait un autre chemin de même longueur possible. Le chemin retourné par l’algorithme dépend en fait de l’ordre dans lequel sont ajouté les amis d’un sommet.

Détails sur l’implémentation

Certains détails n’ont toujours pas été éclairés dans l’algorithme. Comme précisé précédemment, les files sont présentes dans tous les langages, donc pas besoin de les reprogrammer. Cependant, les graphes sont des structures un peu plus sophistiquées et il y a de nombreuses façon de les implémenter.

Dans l’implémentation que je propose plus bas, j’ai choisi de programmer le graphe en utilisant une liste de successeurs. Cela signifie que chaque sommet du graphe contient un lien vers la liste des sommets qui lui sont connectés. En faisant comme ceci, on peut alors accéder facilement aux sommets connectés. Le seul problème est que si on cherche un ami en particulier, il faut parcourir toute la liste d’amis pour le trouver. Avec cette implémentation, il faut également garder à l’esprit que la liste des amis contient uniquement des liens vers les sommets amis, et que la mémoire n’est pas recopiées dans toutes les listes.

Il y a beaucoup d’autre façons d’implémenter des graphes. Une autre façon de faire est d’utiliser un tableau indiquant pour chaque couple de sommet si ils sont connectés (ou amis) ou non. Cette façon de faire utilise plus de mémoire car il y a autant de variables que de connexions possibles dans le graphe.

Enfin, concernant l’implémentation, on peut également parler de l’obtention de la liste finale à partir des sommets d’origine. Pour la liste des sommets d’origines, on peut utiliser une liste d’association qui associe à chaque sommet un lien vers un autre sommet qui est son sommet d’origine. Ensuite, pour construire le chemin, il suffit d’écrire une boucle qui bascule vers le sommet d’origine et va cherche son propre sommet d’origine à chaque étape.

Code

Vous pouvez retrouver une implémentation de l’algorithme ici. L’implémentation a été faite en python. Elle permet de générer aléatoirement un graphe d’amis à partir d’une liste de noms et calcule le plus court chemin pour récupérer l’information dans le graphe. Le code est commenté et le fichier readme donne les détails pour l’exécution du programme.

Vers les algorithmes d’intelligence artificielle

En conclusion, nous avons vu ici un algorithme de base mais qui est également fondamental en informatique. On a fait du parcours de graphe, ce que l’on retrouve dans de nombreux problèmes. Il y a beaucoup de façons de parcourir un graphe, par exemple en largeur, ce qui est présenté ici, ou encore en profondeur, en ajoutant les amis en début de liste d’attente. Ces types de parcours peuvent être utilisés dans de nombreux types de graphes. On considère souvent des parcours d’arbres lorsqu’un un sommet n’est jamais visité deux fois.

Lorsqu’on essaie de résoudre des problèmes de plus en plus complexes, ce qu’on pourrait appeler intelligence artificielle, ces parcours de graphes reviennent très souvent. Par exemple, si on veut créer un programme jouant aux échecs, on va alors explorer le graphe des coups possibles, et essayer de sélectionner le meilleur coup possible. On ne cherche alors plus une simple information mais on cherche à maximiser le score. Dans ce genre de problème, l’algorithme présenté ici est malheureusement très inefficace à cause de la taille du graphe/de l’arbre considéré. Mais des algorithmes très efficaces existent, dont on aura peut-être l’occasion de reparler.